都知道，在平面几何动态问题中出现已知角和“线段分点”时，若求动点的相应轨迹和最值，下妨通过作平行线，移动“角和线段分点”，构造含定值元素的图形确定动点的轨迹和相应最值。现举例三题，大家一起来说说:

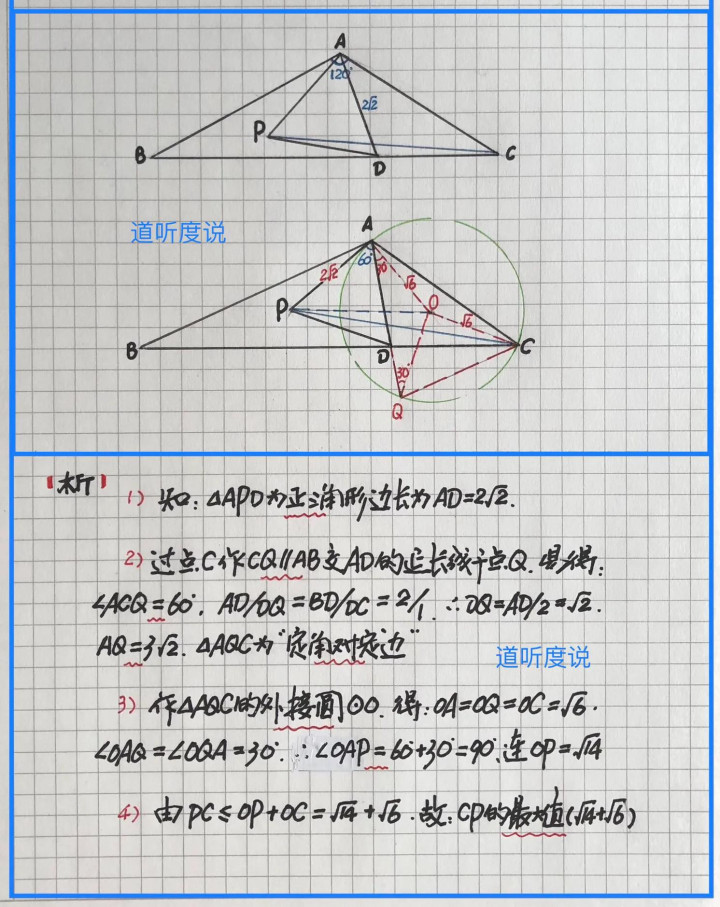
【例1】(如图)在△ABC中，∠BAC=120°，边BC上一点D，满足BD=2DC，AD=2√2，将AD绕点A顺转60°得AP，求CP的最大值

【析】首先，知120°角，线段BC中分点D，BD/DC=2；然后，过点C作AB边的平行线，移动角和线段分点；最后，得“定角对定边”的三角形，确定动点轨迹求得相应最值…具体求解过程如下:

【例2】(如图)△ABC，∠BAC=45°点D在边BC上，且BD=2DC，点E在射线CA上，且√2EC=AB，连DE，求ED/EA的最小值

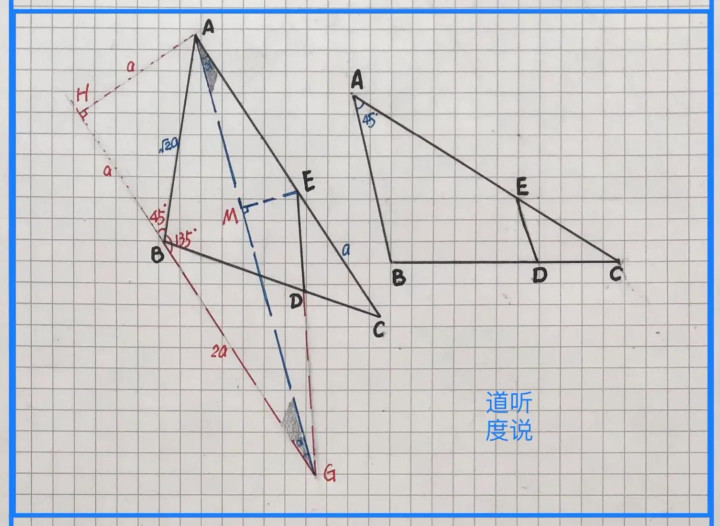
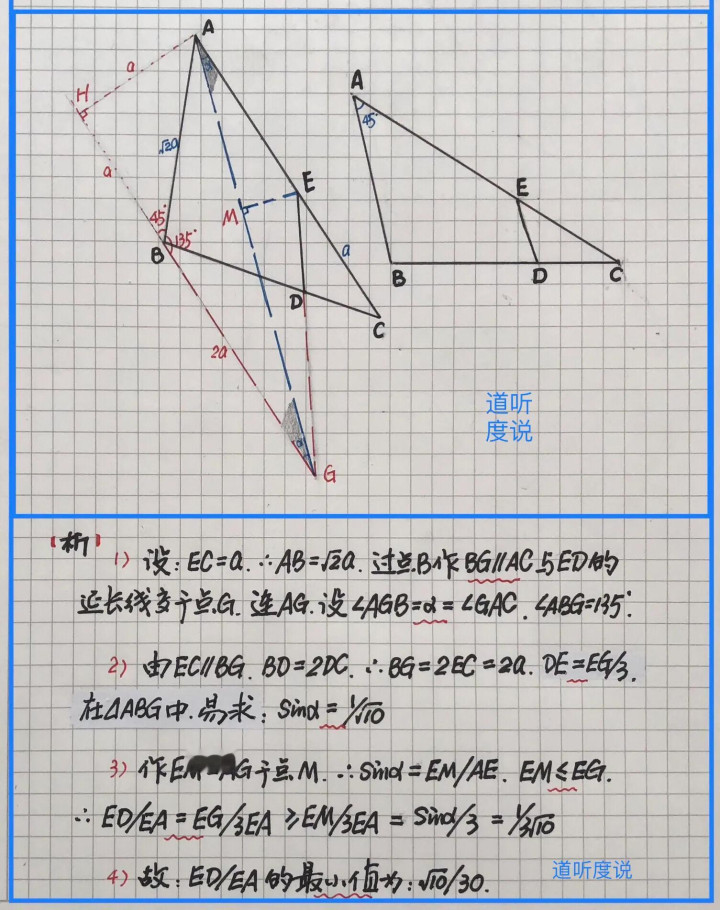
【析】首先，已知45°角，边BC中的分点D；然后，过点B作AC边的平行线，移动角和分线段，得一个形状确定的三角形；最后，在相应的三角形中，利用新确定的角和其正弦的意义求得相应最值…具体求解过程如下:

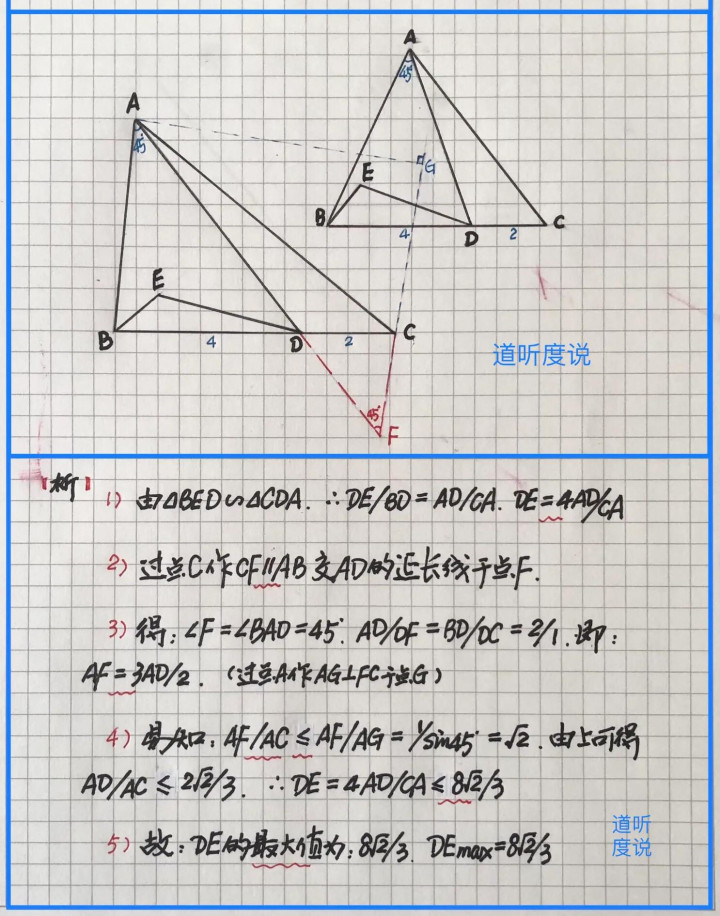
【例3】(如图)△ABC中，点D在BC边上，且BD=2DC=4，平面内一点E(与点A在BC边的同侧)，且满足△BED～△CDA，∠BAD=45°，求线段DE的最大值

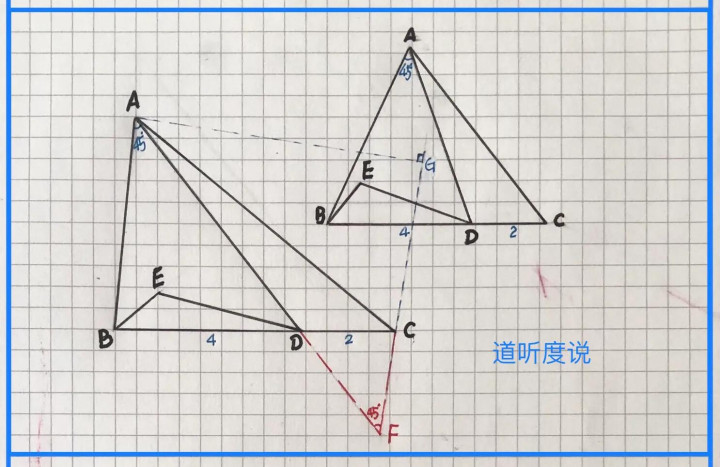
【析】首先，由相似三角形转化为:DE=4(AD/CA)，求(AD/CA)的最值；然后，知45°角和BC边上分点D，作平行线移动已知角和分线段；最后，在含已知角的三角形中，根据角的正弦意义和“斜大于直”，得线段比最值…具体求解过程如下:

以上三例之分析，“道听度说”供参考。